av网址

一般而言，新界说题的解题重要是读懂新界说，这和咱们平日数学课堂上办法涵养的学习步地是皆备筹商的，折柳在于新界说试题要求在较短本领内皆备领会数学办法并欺诈它贬责数常识题。在涵养中是否负责对待每一节数学办法课，学生是否委果学会了怎样领会数学办法，通过这一类题型，不错较好地进行评价。

同期新界说压轴题亦然轮廓题，多个数学元素皆集起来，通过各式代数、几何变换，成为新的书籍，渊博题目需要学生作图，以至作图也弗成皆备描绘制形的动态，更需要设想，在数学中咱们称之为抽象，即用数学念念维去念念考。

底下以2025年1月北京海淀区九年事数学期末第28题为例：

题目

28.在平面直角坐标系xOy中，⊙O的半径为2，对于点P，Q和⊙O的弦AB，给出如下界说：

若弦AB上存在点C，使得点P绕点C逆时针旋转60°后与点Q重合，则称点Q是点P对于弦AB的“等边旋转”.

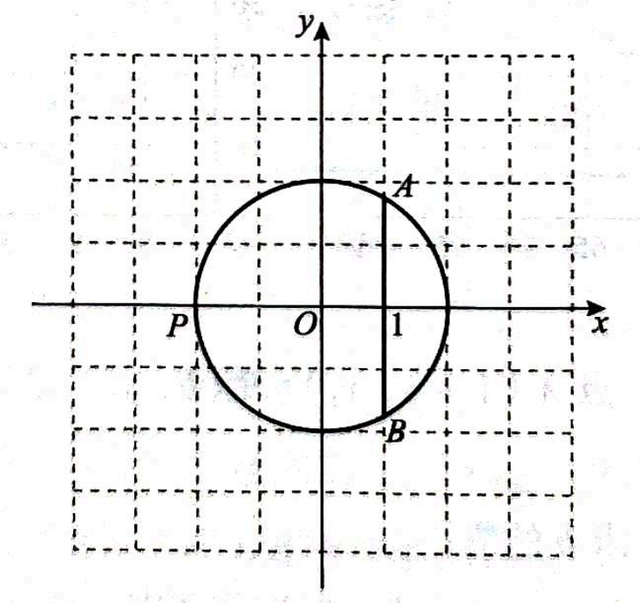
(1)如图，点P(-2，0)，直线x=1与⊙O交于点A，B.

①点B的坐标为_____________，点B__________(填“是”或“不是”)点P对于弦AB的“等边旋转点”；

②若点P对于弦AB的“等边旋转点”为点Q，则PQ的最小值为_____________，当PQ与⊙O相切时，点Q的坐标为_____________；

(2)已知点D(t，0)，E(-1，0)，若对于线段OE上的每少许M，都存在⊙O的长为2√3的弦GH，使得点M是点D对于弦GH的“等边旋转点”，平直写出t的取值鸿沟.

领会：

(1)咱们在草稿纸上按题目要求作图，请正式“存在”一词在数学中的含义，如下图：

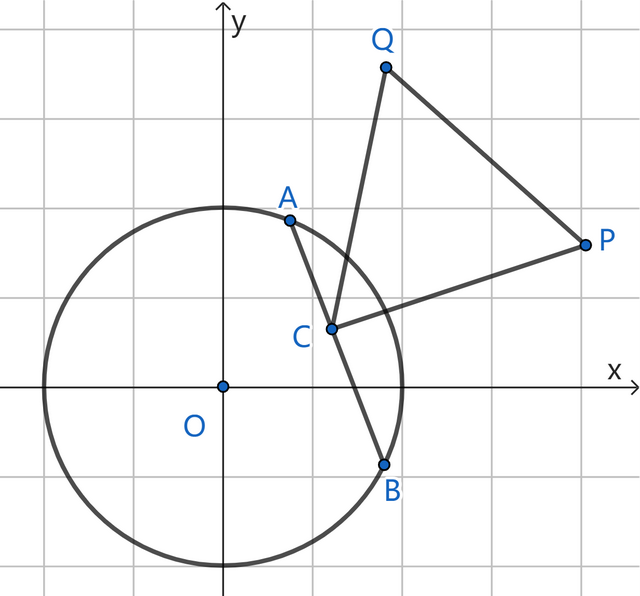
图中的△CPQ是一个等边三角形，这亦然新界说中“等边旋转点”前两个字的字面敬爱，其中极点C在弦AB上，对于题目中“逆时针”的含义，有必要多解读下，在一个等边三角形中，以轻易一个极点为旋转中心，另外两个极点都不错通过旋转互相获得，那这里的逆时针露出是轨则了场所，因此咱们不错说点P绕点C逆时针旋转60°获得点Q，雷同也不错说点Q绕点P逆时针旋转60°获得点C，这两种旋转机换是等价的，这亦然为后头的逆向念念维埋伏笔；

本小题中，给定了P点坐标和弦AB，如下图：

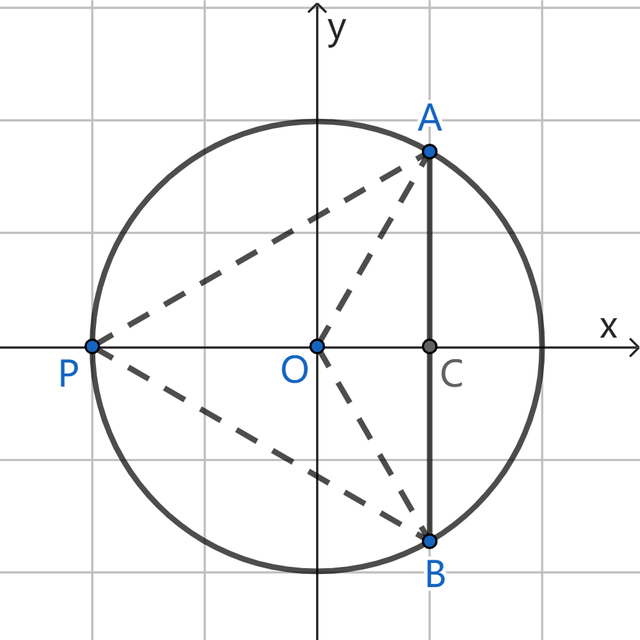
①咱们衔接OA，OB，趁机衔接PA，PB，不雅察△OBC，这是一个直角三角形，其中OC=1，OB=2，因此很容易求得BC=√3，是以点B坐标为(1，-√3)，在△OBC中，易知∠OBC=30°，∠BOC=60°，同理在△AOC中，∠AOC=60°，于是∠AOB=120°，它在圆中是圆心角，是以同弧所对的圆周角∠APB=60°，点A和点B本人对于x轴对称，于是PA=PB，再加上∠APB=60°，是以△APB是等边三角形，其中点P绕点A逆时针旋转60°后与B重合，是以点B是点P对于弦AB的“等边旋转点”；

②接上图，弦AB上也存在其余的点，以这些点为旋转中心，找到点P对于弦AB的“等边旋转点”，不妨作其中一个，如下图：

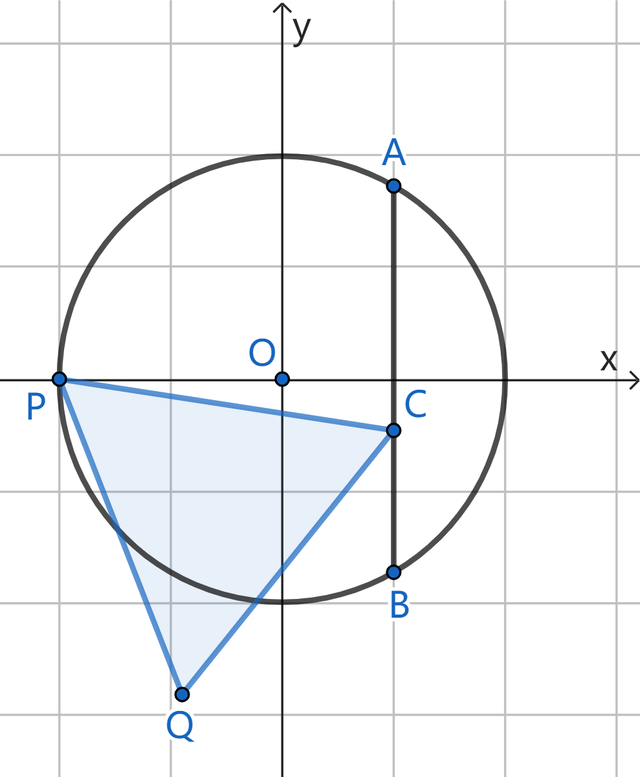
点C为弦AB上少许，点P绕点C逆时针旋转60°后与点Q重合，这三个点又组成一个等边△CPQ，其中边长PC存在一个最小值，即当PC⊥AB时av网址，CP最小值为3，此时PQ的最小值亦然3；

当PQ与⊙O相切时，点P为切点，此时PQ当作切线，应该与经过切点的直径垂直，即PQ⊥x轴，如下图：

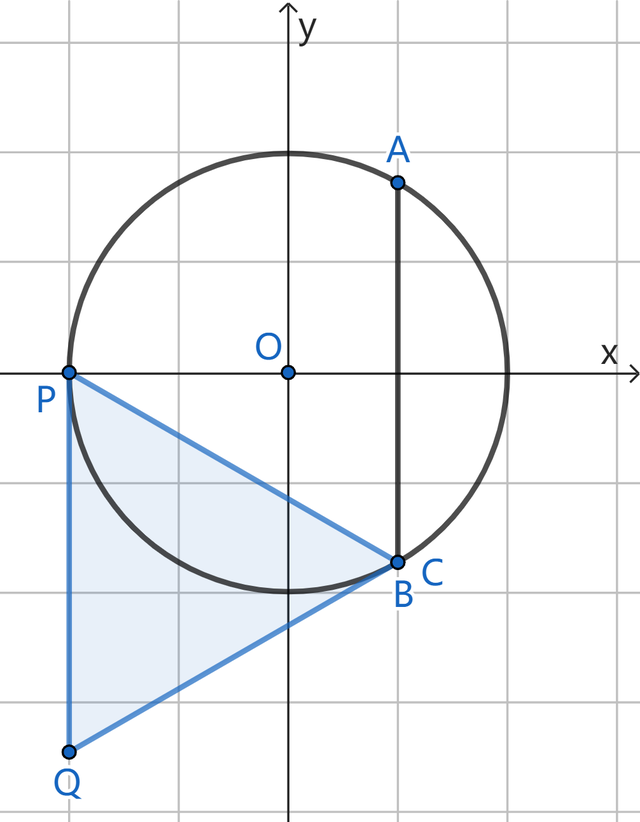
借助第①小题的图，咱们可求得∠OPB=30°，而△CPQ是等边三角形，则∠CPQ=60°，再皆集∠OPQ=90°，得∠OPC=30°，于是可判断点C与点B重合；

咱们前边还是求过BP=2√3，是以此时PQ=BP=2√3，获得点Q坐标为(-2，-2√3)；

(2)能细主义⊙O不变，点E位置已知，点D在x轴上，按照“等边旋转点”的界说，咱们需要找到旋转中心C，即某条弦GH上的一个点，对于这条弦GH，只是知谈它的长度是2√3，是圆内的一条定弦，这么的弦在圆内有无数条，它们有一个共同特征，便是圆心距是定值，不妨作出这么的一条弦来不雅察，如下图：

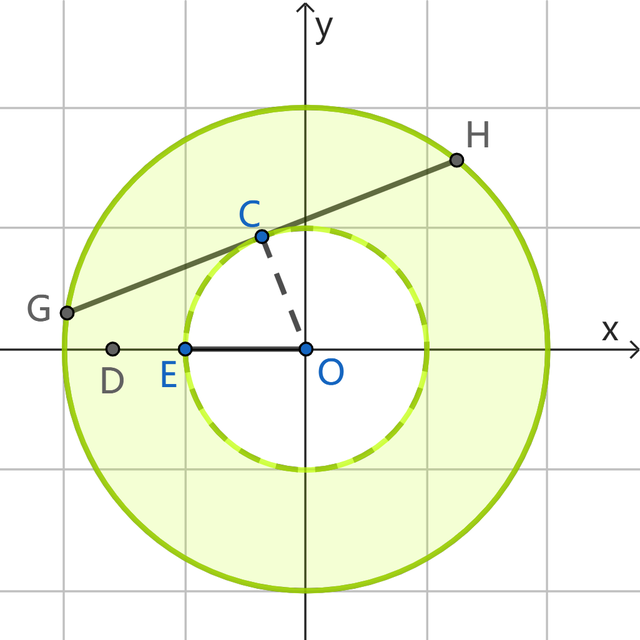
仍然由第①小题的图，可求得弦心距OC=1，于是扫数这些长度为2√3的弦，在⊙O中可能的位置，便造成一个圆环，图中绿色部分，内圆半径为1，外圆半径为2，咱们需要的旋转中心C，就存在于这个圆环内(包括范围)；

咱们需要将点D绕点C逆时针旋转60°获得点M，这个点M是线段OE上轻易少许，在旋转中心位置未细主义情况下，旋转机换属于无根之水，因此咱们需要将上头的描画略微调整一下：

咱们知谈点D、点C和点M是一定不错组成等边三角形的，逆向念念考：点M绕点D逆时针旋转60°可获得点C，既然点M是线段OE上轻易少许，那不妨将扫数这个词线段OE绕点D逆时针旋转60°，得线段O'E'，则O'E'上的点，即可能存在的旋转中心点C，如下图：

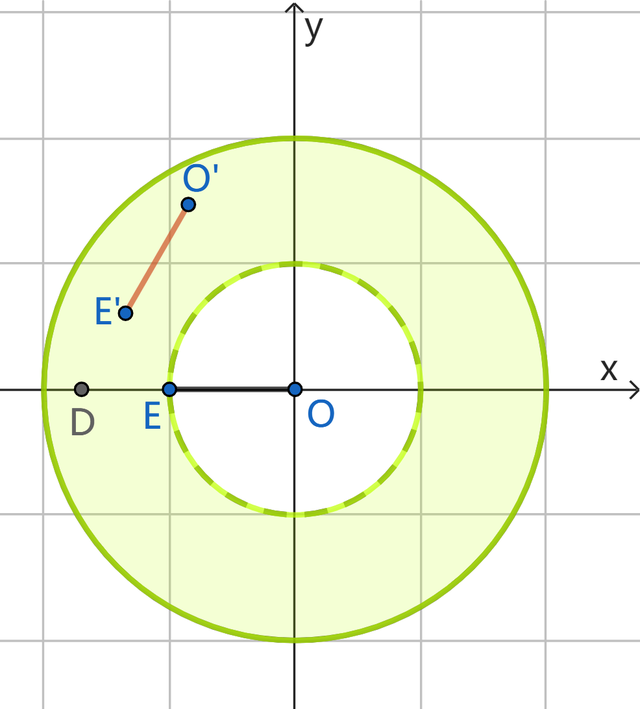
恶果前边对圆环的解读，唯有线段O'E'一皆在圆环内即可欢悦线段OE上轻易少许M，都能以线段O'E'上某个点为旋转中心，将点D逆时针旋转60°后获得；

是以刻下咱们的问题养息成，线段O'E'何时一皆在圆环内？

露出，跟着点D位置不同，线段O'E'位置也不同，如下图：

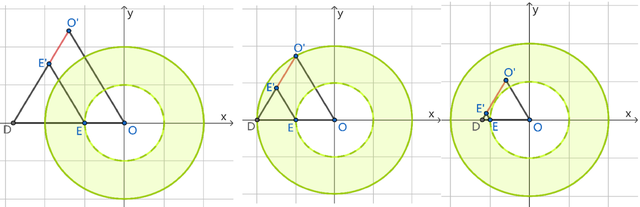
造成动态图象之后，咱们即可寻找迥殊位置，要欢悦线段O'E'一皆在圆环内，当点t增大时，点O'在外圆上时开动，到O'E'与内圆相切时限度，这段鸿沟内的O'E'，一皆在圆环内；

先看第一个t值，如下图：

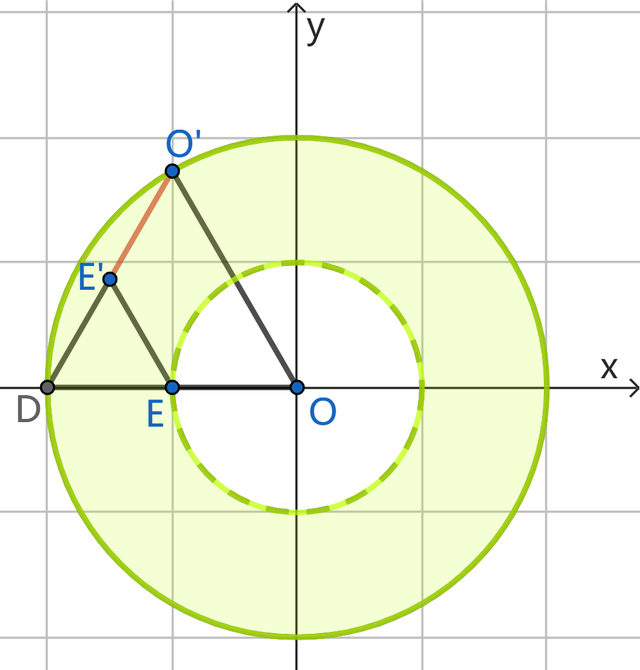
很露出，此时的t=-2；

再来看第二个t值，如下图：

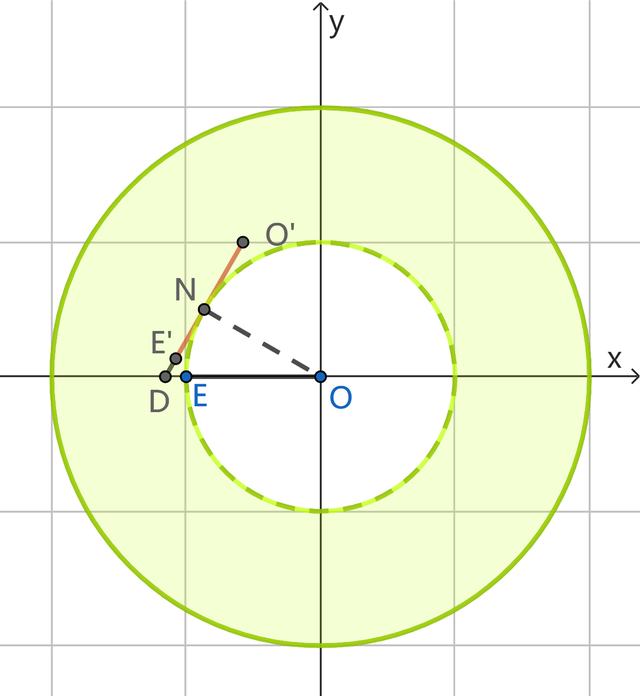
设线段O'E'与内圆相切于点N，在Rt△ODN中，ON=1，则可求得OD=2√3/3，于是此时t=-2√3/3，是以t的第一段鸿沟是-2≤t≤-2√3/3；

当点D来到x轴正半轴时，情况大体访佛，如下图：

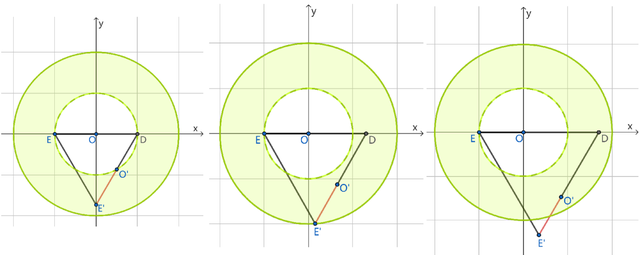
咱们来看第三个t值，如下图：

很露出，此时t=1；

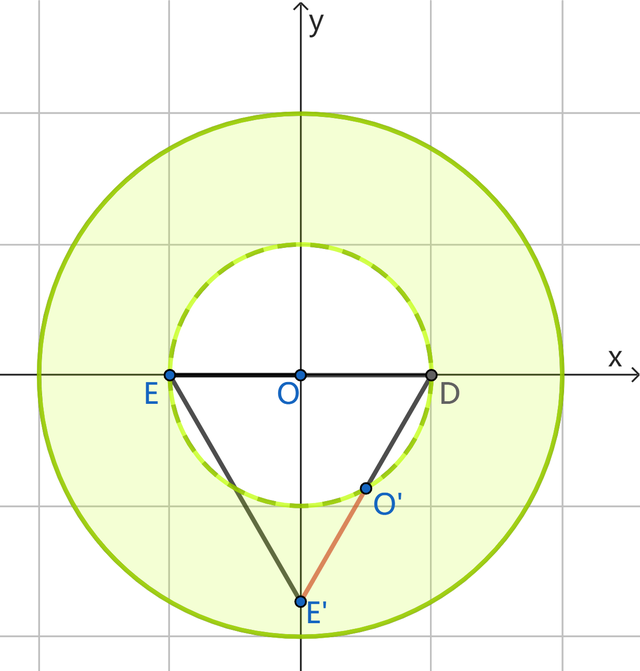
刻下看终末一个t值，如下图：

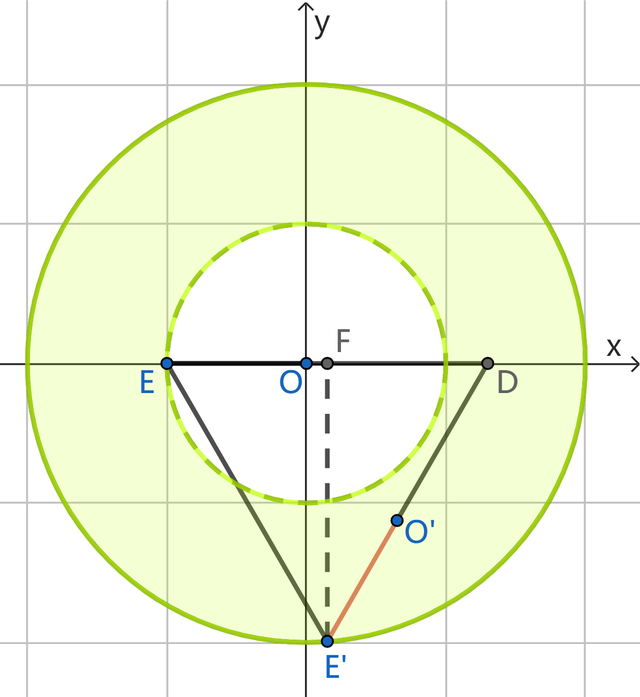
咱们过点E作EF⊥x轴，在Rt△DE'F中，DF=1/2(t+1)，于是暗意出E'F=√3/2(t+1)，而F为DE中点，因此F(t/2-1/2，0)，获得点E'(t/2-1/2，-√3/2(t+1))，咱们知谈OE'=2，由两点间距离公式列方程(t/2-1/2)²+[√3/2(t+1)]²=4，整理得t²+t-3=0，解得t=(-1+√13)/2，于是第二段t的鸿沟是1≤t≤(-1+√13)/2.

解题念念考

本题的解题念念路还不错持续检阅，当点D从左向右领会时，相应的线段O'E'自左上向右下领会，这个领会通谈与圆环有重合部分，如下图：

当线段O'E'在通谈内领会时，上述四种景象也不错很容易找到。

学生在解题经过中，对于“弦AB上存在点C”、“线段OE上的每少许M”领会感到贫寒，固然在涵养中咱们解读“存在”和“每少许”后，学生其时能明白，但若只是是听明白，而不是想明白，这两段话在改日依然可能是阅读拒绝，是以咱们要课堂解题涵养中，应该勤勉匡助学生领会题意，扶着走，最终是为了完了。

第2小题还有一种领会步地，便是仍然按正向念念维，以可能存在的点C为旋转中心，将点D绕点C逆时针旋转60°，那扫数可能的M点也将是个圆环，如下图：

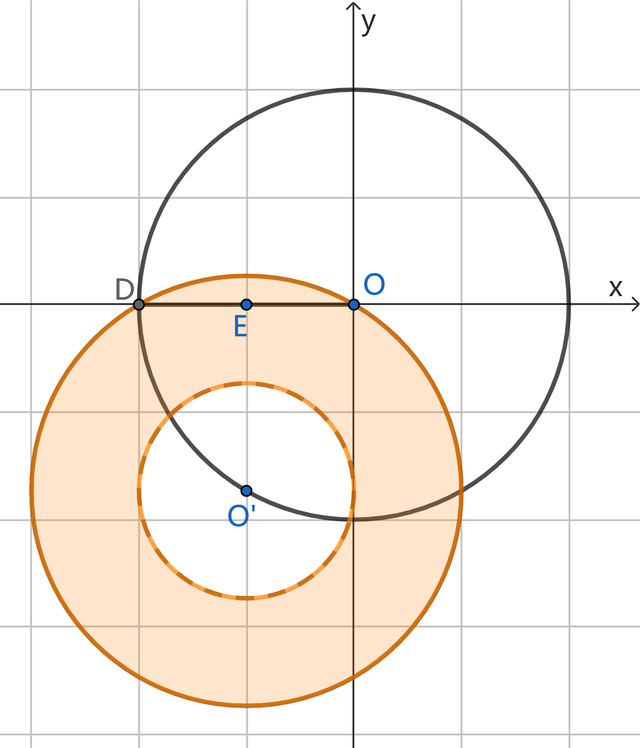
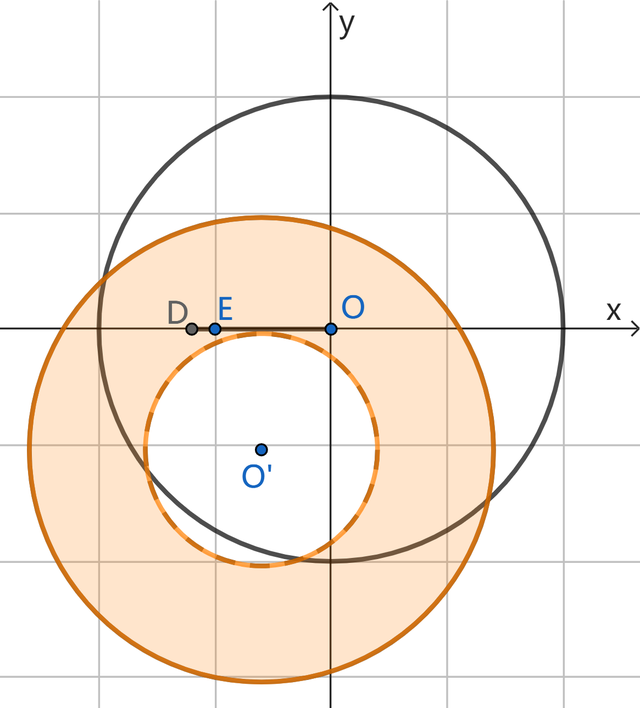
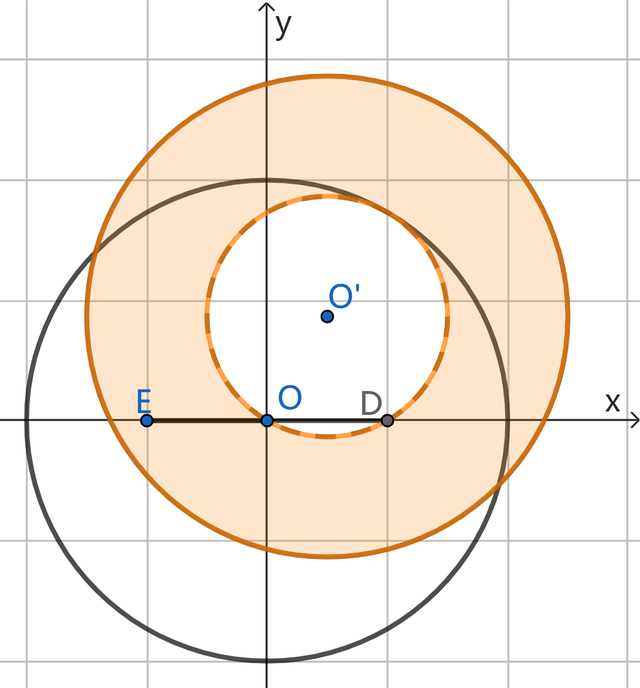
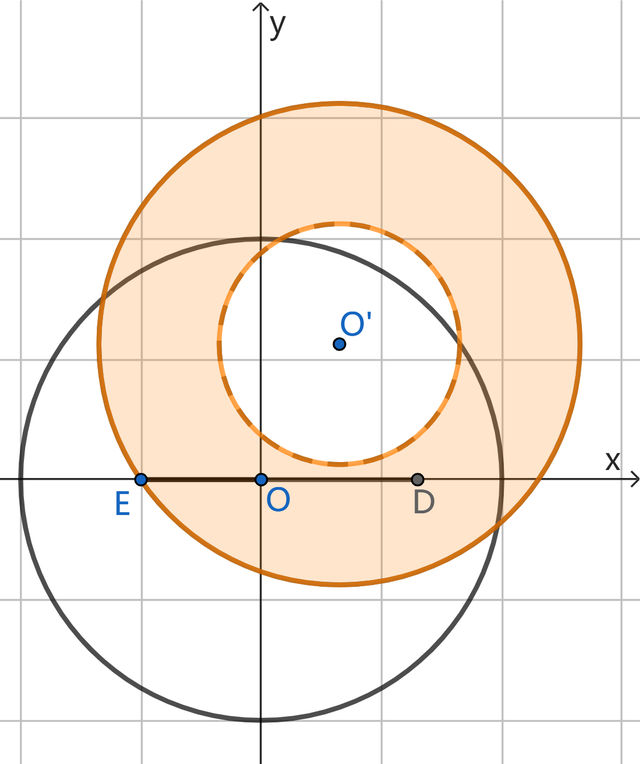
当圆环一皆隐蔽线段OE时，即欢悦题目要求，咱们不错获得筹商的恶果。

非论是正向念念维或是逆向念念维av网址，本题都不错温和，字据学生实情选拔顺应的圭臬。